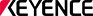Calculating Capacitance
The previous sections covered electric charge and field. Capacitance describes how much charge can be stored. This section covers the basics of capacitance as well as how to calculate it.
What is capacitance?
Capacitance is the amount of electric charge that can be stored in a capacitor or other device. It is called electrical capacity.
The proportional relationship between the potential and actual amount of charge of a charged object can be described as follows:
Q=CV[C]
The proportionality constant C is the capacitance, and the unit is farads [F].
If the amount of charge is 1 C and the potential difference is 1 V, the capacitance will be 1 F. However, since this unit is too large for practical use, microfarads (μF), which are one millionth of 1 F (10-6), or picofarads (pF), one trillionth of 1 F (10-12), are commonly used.
1 F = 106 μF = 1012 pF
The figure shows an explanation of capacitance by likening it to water in a container.
Let’s suppose that the amount of water in the container is the amount of charge, and the water level is the potential, and the area of the bottom of the container is the capacitance.
When you put the same amount of water into a container with a small base area and a container with a larger base area, the water level rises quickly in the former while the rise in water level is moderate in the latter. In short, if you think of a charged object as a container holding charge, the capacitance describes the size or capacity of that container.
The difference between water and electrons in this example is that water flows from a higher to a lower place, and eventually the water level of the two places becomes the same, while in the case of electrons, the potential of the side that released electrons rises and the side that received electrons has a lowered potential. This means that the former is positively charged while the latter is negatively charged.
Calculating capacitance
To calculate capacitance, the following formulas can be used depending on the size, shape, and ambient environment of the charged object.
Spherical conductors
A spherical conductor with a radius a [m] receiving a charge [Q] will have the following surface potential:
V = Q/4πε0a[V]
Capacitance will be:
C = Q/V=4πε0a[F]
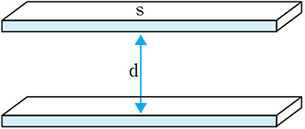
Parallel conductor plates
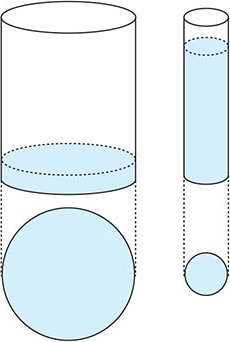
As shown in the picture, in the case of two parallel conductor plates with an area S [m2] separated by a distance d [m], with one plate receiving a charge +Q while the other receives -Q, the electric field strength acting between those electrodes is:
(Charge density σ = Q/S)
The potential difference between the electrodes [V] is calculated as:
V = Ed = dQ/Sε0
Therefore, the capacitance is as follows:
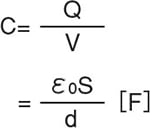
If there is an insulator between the conductor plates, the (relative permittivity of insulator) capacitance can be expressed as follows:
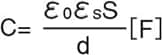
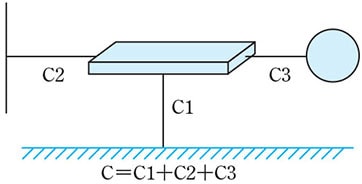
Example 1: Capacitance of charged object
If there are multiple conductors approaching a conductor that is grounded as shown in the picture, the capacitance of the object is the sum of all capacitances of the conductors.
Example 2: Insulator
Cases where a conductor plate is closely attached to the back of an insulator film and grounded.
An example case where an insulator file (relative permittivity) with a thickness d [m] is closely attached to a grounded conductor and has a charge Q [C/m2] on the surface of the film.
The back of the film has an opposite polarity to that of the conductor plate it is closely attached to and a charge of the same value as that of the conductor plate.
The arrangement of the charges is the same as that in the case of two parallel plates charged with a charge density σ as shown below.
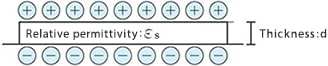
The insulator surface charge Vs in this state is as follows:
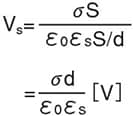
Example 3: Insulator films with different thickness
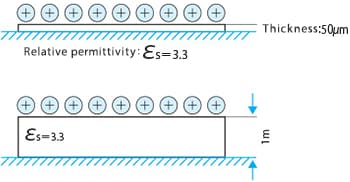
If a polyimide film (thickness: 100 [μm], relative permittivity = 3.3) that is closely attached to a grounded conductor plate as shown in the picture below has a surface charge density σ (= 1×10-5 [C/m2]), the surface potential is:
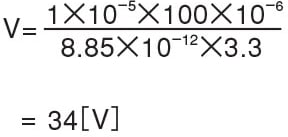
Under the same conditions, if the thickness of the film is 1 [mm],
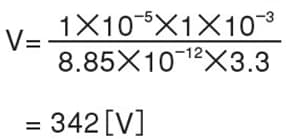
Films with different thickness have the same relative permittivity and charge density, but have a significant difference in surface potential.